I must confess… I’m terrible at keeping tabs on my belongings.
In grade 3, I left the house with a backpack, pants, and my gym shorts, and only came back home with my gym shorts. This has been a common theme in my life. 😅
The other day I couldn’t find my earbuds and spent literally 30 minutes looking for them around the house (and no, I don’t live in a mansion).
After some time, I became convinced that I must have lost them. It wouldn’t surprise me if I had.
That’s when I had a flashback to all the times my friends and colleagues have said the clever little catchphrase
Absense of Evidence is not evidence of absence
At first glance, I guess that makes sense.
Something’s still bugged me though… Isn’t there any kind of meaning to my search for my earbuds?
Sure, absence of evidence is not proof of absence, but surely, it is some kind of evidence! If I didn’t look at all where my earbuds may have been then, sure, that’s not evidence of jack shit, but I looked where I expected it to be, and it wasn’t there!
Wait a minute… This is a pretty simple assertion. Thanks to a recent video by 3Blue1Brown, I got inspired to use my Statistics 101 skills and test this claim using Bayes’ Theorem.
Let’s break it down, shall we?
What is Evidence?
I think it would be fair to say that evidence is any information that reduces one’s uncertainty about a particular belief.
At the end of the day, the world is as it is, and evidence is just for us feeble humans to convince ourselves we understand it.
Armed with that definition, we can now translate some simple facts to probability notation.
English: I would never find my earbuds if they were absent.
Math: P(Find|Absent) = 0 and P(~Find|Absent) = 1
English: If I find my earbuds, that means they can’t be absent.
Math: P(Absent|Find) = 0 and P(~Absent|Find) = 1
Now, what I want to know is the probability of absence given I haven’t found them after looking and whether that is different than the probability of absence without ever looking at all.
Recall that Bayes’ theorem states
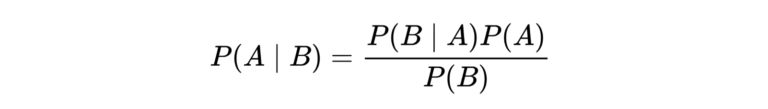
SinceP(Absent|~Find) = P(~Find|Absent) P(Absent) /P(~Find)
P(~Find|Absent) = 1 this implies P(Absent|~Find) = P(Absent) / P(~Find)Now, here’s the tricky bit…Let’s assume for a moment that, I already knew that I couldn’t ever find my earbuds cause they vanished out of existence. In this case, P(~Find) = 1 which would mean P(Absent|~Find) = P(Absent) In English, that would mean the fact that I have looked and haven’t found my earbuds has no bearing on the probability of them being absent.In reality, P(~Find)< 1 because, why in the world would I be looking if I didn’t believe there was a chance of finding them?So now, the only obvious conclusion is that the probability that my earbuds are absent after not finding them must be greater than the probability that it is absent.P(Absent|~Find) > P(Absent)That’s it. The absence of evidence is, in fact, evidence of absence (just not proof of absence.)
Conclusion
You might scoff at my silly example.
Losing your earbuds or keys is inconsequential.
Unfortunately, this misconception rears its ugly head EVERYWHERE, and the topics in question are far from inconsequential.
In a NATO conference in 2002, the then Secretary of Defence, Donald Rumsfeld proclaimed that the military action in Iraq in search of weapons of mass destruction was justified, despite the fact, that after multiple inspections and assessment of various intelligence, no evidence for such weapons was discovered.
The very foundation upon which we built scientific hypotheses — regular old hypothesis testing — depends on being able to assume that in certain contexts of inquiry an absence of evidence can serve as evidence of absence.
So… The next time you’re having that heated argument about the existence of [name your entity — think on it for a second], keep in mind that the longer we keep looking without finding, the more evidence we are accumulating that it does not exist.
Have some strong opinions on this topic? Comment and don’t hold back!

2 Responses
This is so asinine. Read some Taleb – he’s arrogant but at least he has logic.
Hi Katrina,
Thank you for your input.
I’m curious which part you felt the logic doesn’t follow?